Fundamental Data Structures in JavaScript

A simple to follow guide to Lists Stacks and Queues, with animated gifs, diagrams, and code examples!

Fundamental Data Structures in JavaScript

A simple to follow guide to Lists Stacks and Queues, with animated gifs, diagrams, and code examples!

Linked Lists

In the university setting, it’s common for Linked Lists to appear early on in an undergraduate’s Computer Science coursework. While they don’t always have the most practical real-world applications in industry, Linked Lists make for an important and effective educational tool in helping develop a student’s mental model on what data structures actually are to begin with.

Linked lists are simple. They have many compelling, reoccurring edge cases to consider that emphasize to the student the need for care and intent while implementing data structures. They can be applied as the underlying data structure while implementing a variety of other prevalent abstract data types, such as Lists, Stacks, and Queues, and they have a level of versatility high enough to clearly illustrate the value of the Object Oriented Programming paradigm.

They also come up in software engineering interviews quite often.

What is a Linked List?

A Linked List data structure represents a linear sequence of “vertices” (or “nodes”), and tracks three important properties.

Linked List Properties:

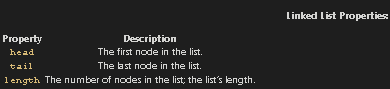
The data being tracked by a particular Linked List does not live inside the Linked List instance itself. Instead, each vertex is actually an instance of an even simpler, smaller data structure, often referred to as a “Node”.

Depending on the type of Linked List (there are many), Node instances track some very important properties as well.

Linked List Node Properties:

Property Description value: The actual value this node represents.nextThe next node in the list (relative to this node).previousThe previous node in the list (relative to this node).

NOTE: The previous property is for Doubly Linked Lists only!

Linked Lists contain ordered data, just like arrays. The first node in the list is, indeed, first. From the perspective of the very first node in the list, the next node is the second node. From the perspective of the second node in the list, the previous node is the first node, and the next node is the third node. And so it goes.

“So…this sounds a lot like an Array…”

Admittedly, this does sound a lot like an Array so far, and that’s because Arrays and Linked Lists are both implementations of the List ADT. However, there is an incredibly important distinction to be made between Arrays and Linked Lists, and that is how they physically store their data. (As opposed to how they represent the order of their data.)

Recall that Arrays contain contiguous data. Each element of an array is actually stored next to it’s neighboring element in the actual hardware of your machine, in a single continuous block in memory.

An Array’s contiguous data being stored in a continuous block of addresses in memory.

Unlike Arrays, Linked Lists contain non-contiguous data. Though Linked Lists represent data that is ordered linearly, that mental model is just that — an interpretation of the representation of information, not reality.

In reality, in the actual hardware of your machine, whether it be in disk or in memory, a Linked List’s Nodes are not stored in a single continuous block of addresses. Rather, Linked List Nodes live at randomly distributed addresses throughout your machine! The only reason we know which node comes next in the list is because we’ve assigned its reference to the current node’s next pointer.

A Singly Linked List’s non-contiguous data (Nodes) being stored at randomly distributed addresses in memory.

For this reason, Linked List Nodes have no indices, and no random access. Without random access, we do not have the ability to look up an individual Linked List Node in constant time. Instead, to find a particular Node, we have to start at the very first Node and iterate through the Linked List one node at a time, checking each Node’s next Node until we find the one we’re interested in.

So when implementing a Linked List, we actually must implement both the Linked List class and the Node class. Since the actual data lives in the Nodes, it’s simpler to implement the Node class first.

Types of Linked Lists

There are four flavors of Linked List you should be familiar with when walking into your job interviews.

Linked List Types:

Note: These Linked List types are not always mutually exclusive.

For instance:

Any type of Linked List can be implemented Circularly (e.g. A Circular Doubly Linked List).
A Doubly Linked List is actually just a special case of a Multiply Linked List.

You are most likely to encounter Singly and Doubly Linked Lists in your upcoming job search, so we are going to focus exclusively on those two moving forward. However, in more senior level interviews, it is very valuable to have some familiarity with the other types of Linked Lists. Though you may not actually code them out, you will win extra points by illustrating your ability to weigh the tradeoffs of your technical decisions by discussing how your choice of Linked List type may affect the efficiency of the solutions you propose.

Linked List Methods

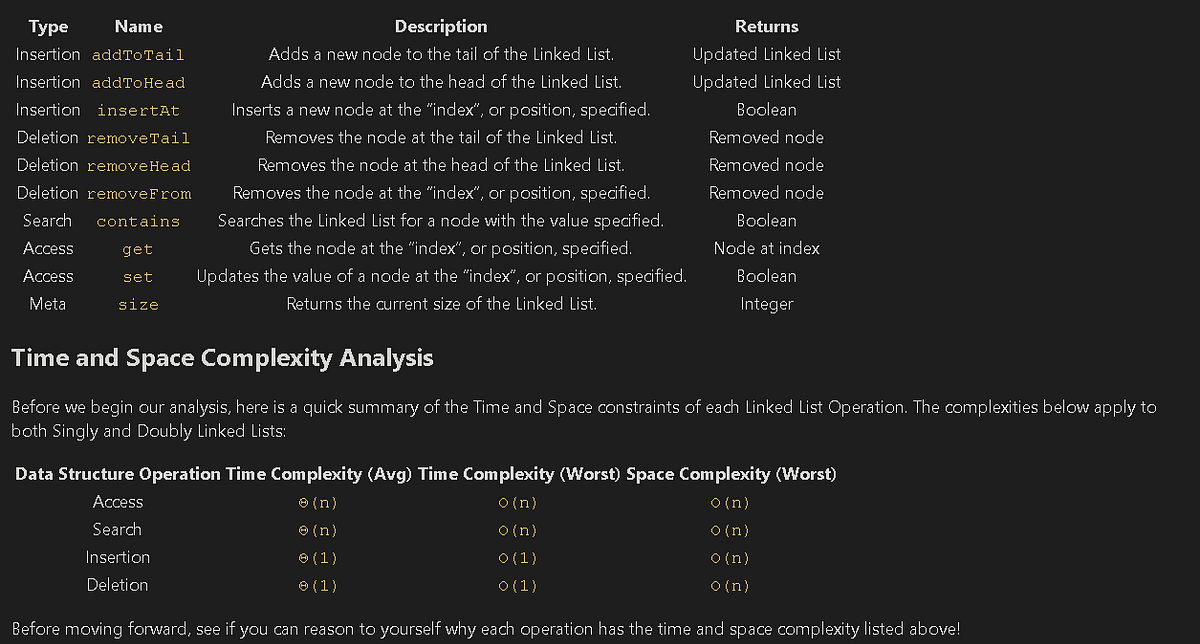
Linked Lists are great foundation builders when learning about data structures because they share a number of similar methods (and edge cases) with many other common data structures. You will find that many of the concepts discussed here will repeat themselves as we dive into some of the more complex non-linear data structures later on, like Trees and Graphs.

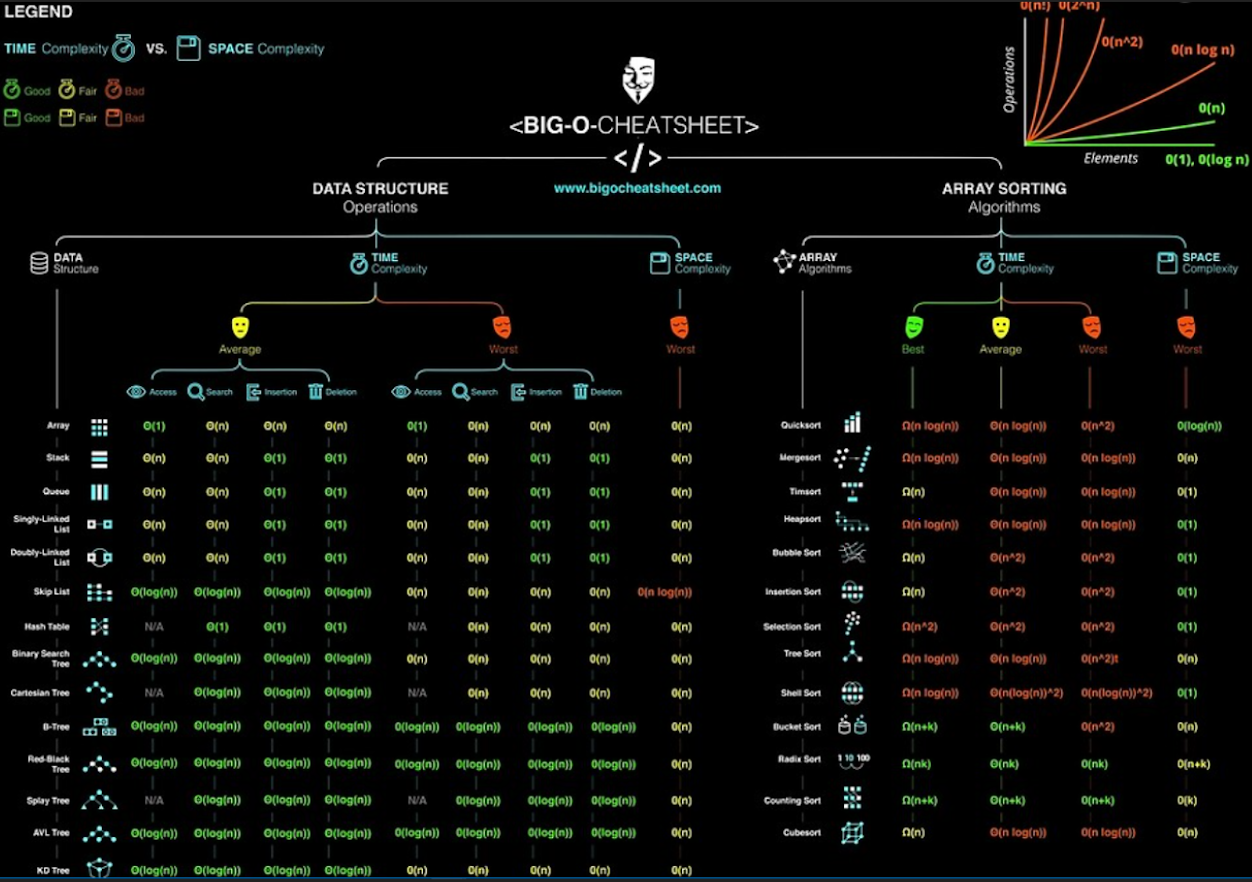
Time and Space Complexity Analysis

Before we begin our analysis, here is a quick summary of the Time and Space constraints of each Linked List Operation. The complexities below apply to both Singly and Doubly Linked Lists:

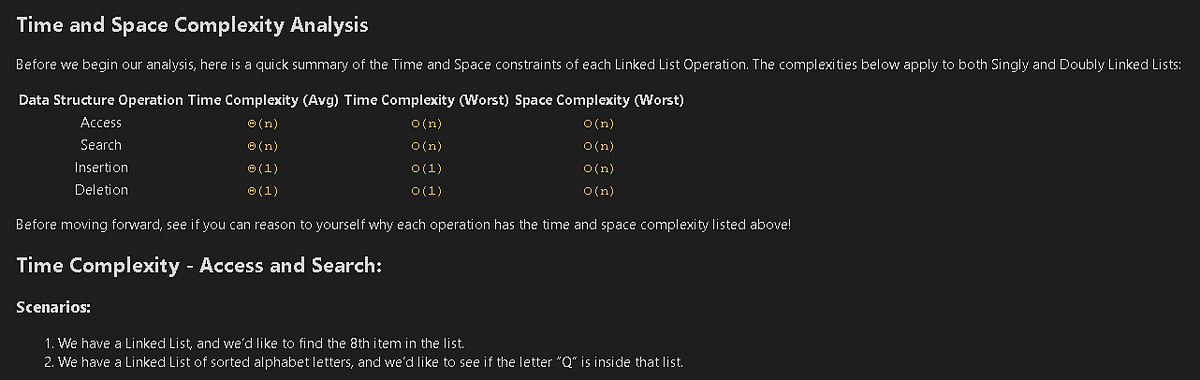
Before moving forward, see if you can reason to yourself why each operation has the time and space complexity listed above!

Time Complexity — Access and Search

Scenarios

We have a Linked List, and we’d like to find the 8th item in the list.
We have a Linked List of sorted alphabet letters, and we’d like to see if the letter “Q” is inside that list.

Discussion

Unlike Arrays, Linked Lists Nodes are not stored contiguously in memory, and thereby do not have an indexed set of memory addresses at which we can quickly lookup individual nodes in constant time. Instead, we must begin at the head of the list (or possibly at the tail, if we have a Doubly Linked List), and iterate through the list until we arrive at the node of interest.

In Scenario 1, we’ll know we’re there because we’ve iterated 8 times. In Scenario 2, we’ll know we’re there because, while iterating, we’ve checked each node’s value and found one that matches our target value, “Q”.

In the worst case scenario, we may have to traverse the entire Linked List until we arrive at the final node. This makes both Access & Search Linear Time operations.

Time Complexity — Insertion and Deletion

Scenarios

We have an empty Linked List, and we’d like to insert our first node.
We have a Linked List, and we’d like to insert or delete a node at the Head or Tail.
We have a Linked List, and we’d like to insert or delete a node from somewhere in the middle of the list.

Discussion

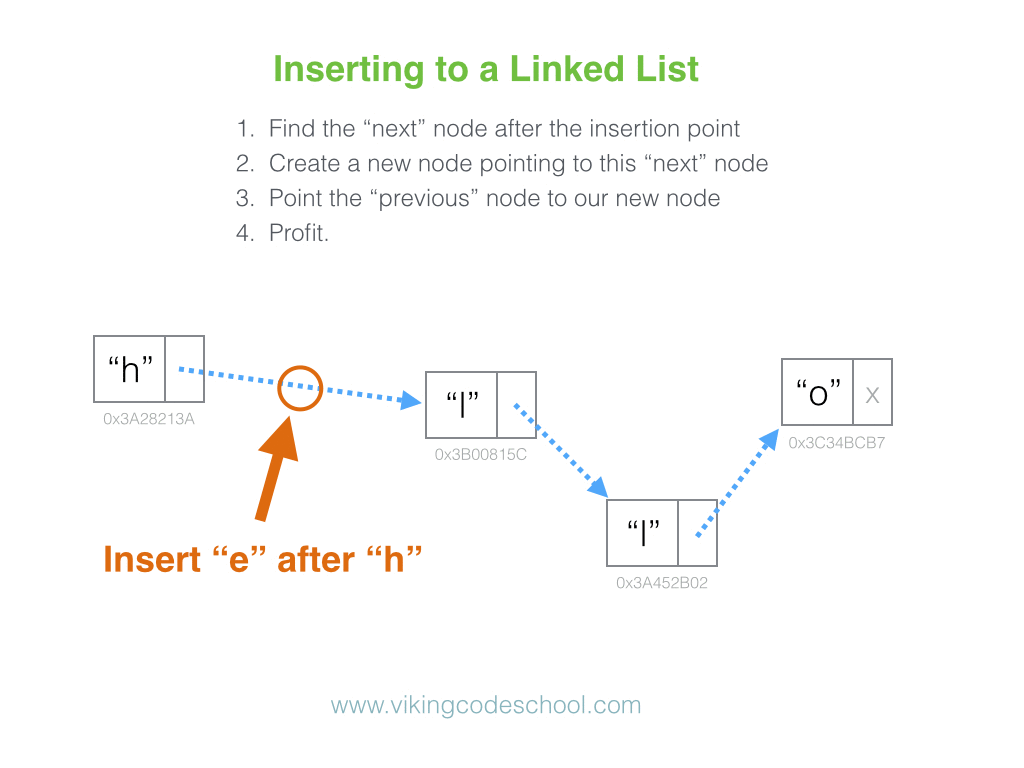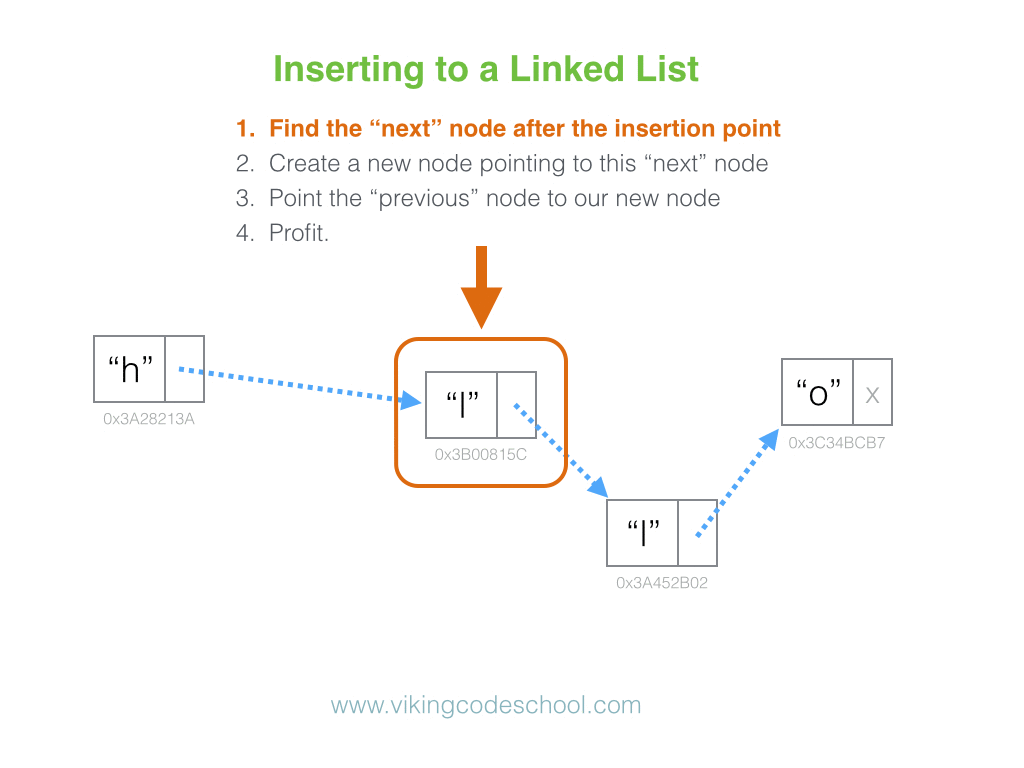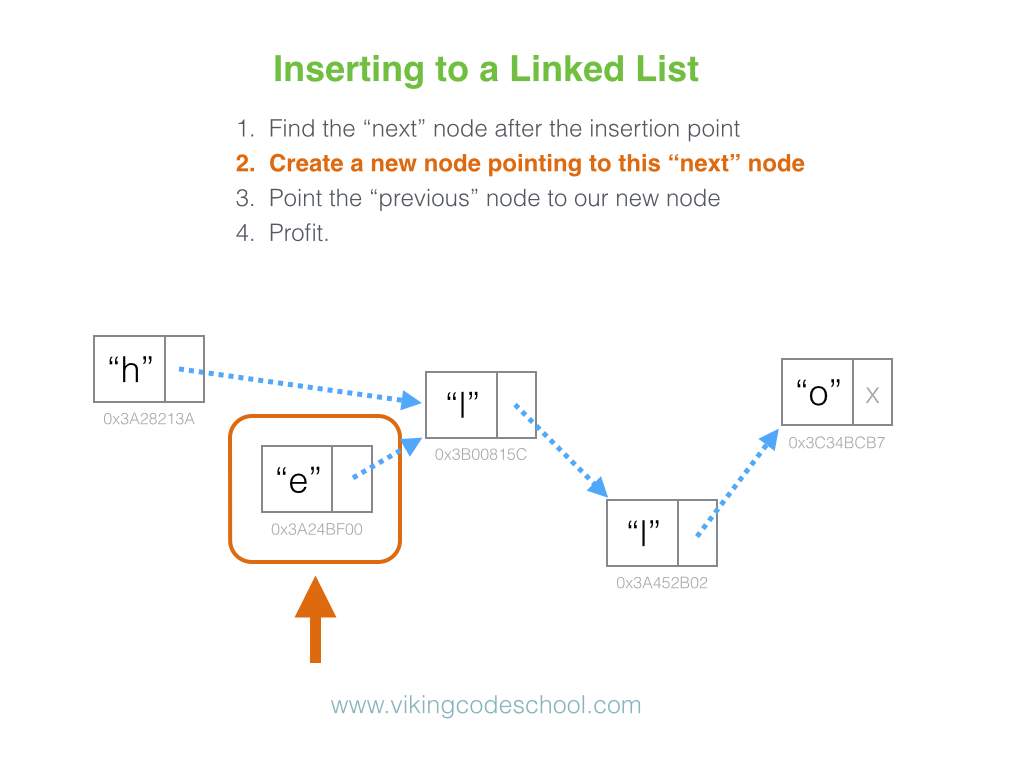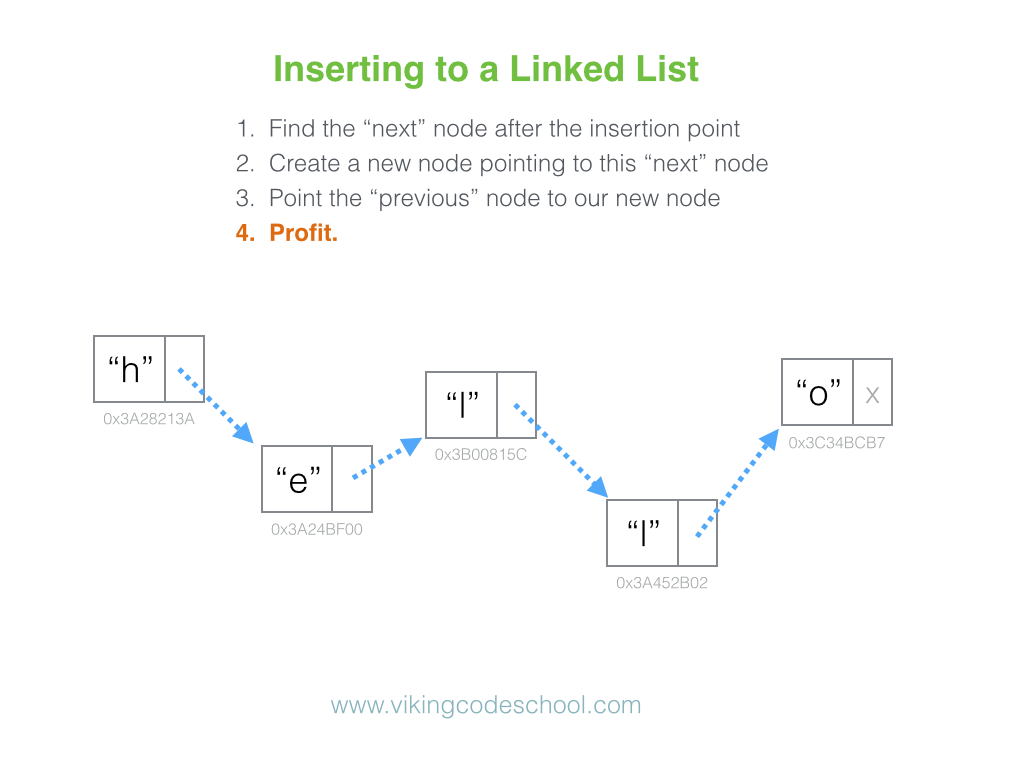
Since we have our Linked List Nodes stored in a non-contiguous manner that relies on pointers to keep track of where the next and previous nodes live, Linked Lists liberate us from the linear time nature of Array insertions and deletions. We no longer have to adjust the position at which each node/element is stored after making an insertion at a particular position in the list. Instead, if we want to insert a new node at position i, we can simply:

Create a new node.
Set the new node’s next and previous pointers to the nodes that live at positions i and i - 1, respectively.
Adjust the next pointer of the node that lives at position i - 1 to point to the new node.
Adjust the previous pointer of the node that lives at position i to point to the new node.

And we’re done, in Constant Time. No iterating across the entire list necessary.

“But hold on one second,” you may be thinking. “In order to insert a new node in the middle of the list, don’t we have to lookup its position? Doesn’t that take linear time?!”

Yes, it is tempting to call insertion or deletion in the middle of a Linked List a linear time operation since there is lookup involved. However, it’s usually the case that you’ll already have a reference to the node where your desired insertion or deletion will occur.

For this reason, we separate the Access time complexity from the Insertion/Deletion time complexity, and formally state that Insertion and Deletion in a Linked List are Constant Time across the board.

Note: Without a reference to the node at which an insertion or deletion will occur, due to linear time lookup, an insertion or deletion in the middle of a Linked List will still take Linear Time, sum total.

Space Complexity

Scenarios

We’re given a Linked List, and need to operate on it.
We’ve decided to create a new Linked List as part of strategy to solve some problem.

Discussion

It’s obvious that Linked Lists have one node for every one item in the list, and for that reason we know that Linked Lists take up Linear Space in memory. However, when asked in an interview setting what the Space Complexity of your solution to a problem is, it’s important to recognize the difference between the two scenarios above.

In Scenario 1, we are not creating a new Linked List. We simply need to operate on the one given. Since we are not storing a new node for every node represented in the Linked List we are provided, our solution is not necessarily linear in space.

In Scenario 2, we are creating a new Linked List. If the number of nodes we create is linearly correlated to the size of our input data, we are now operating in Linear Space.

Note: Linked Lists can be traversed both iteratively and recursively. If you choose to traverse a Linked List recursively, there will be a recursive function call added to the call stack for every node in the Linked List. Even if you’re provided the Linked List, as in Scenario 1, you will still use Linear Space in the call stack, and that counts.

Stacks and Queues

Stacks and Queues aren’t really “data structures” by the strict definition of the term. The more appropriate terminology would be to call them abstract data types (ADTs), meaning that their definitions are more conceptual and related to the rules governing their user-facing behaviors rather than their core implementations.

For the sake of simplicity, we’ll refer to them as data structures and ADTs interchangeably throughout the course, but the distinction is an important one to be familiar with as you level up as an engineer.

Now that that’s out of the way, Stacks and Queues represent a linear collection of nodes or values. In this way, they are quite similar to the Linked List data structure we discussed in the previous section. In fact, you can even use a modified version of a Linked List to implement each of them. (Hint, hint.)

These two ADTs are similar to each other as well, but each obey their own special rule regarding the order with which Nodes can be added and removed from the structure.

Since we’ve covered Linked Lists in great length, these two data structures will be quick and easy. Let’s break them down individually in the next couple of sections.

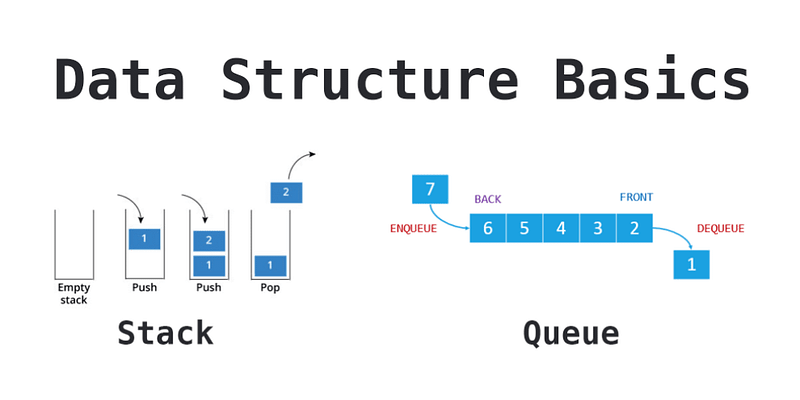
What is a Stack?

Stacks are a Last In First Out (LIFO) data structure. The last Node added to a stack is always the first Node to be removed, and as a result, the first Node added is always the last Node removed.

The name Stack actually comes from this characteristic, as it is helpful to visualize the data structure as a vertical stack of items. Personally, I like to think of a Stack as a stack of plates, or a stack of sheets of paper. This seems to make them more approachable, because the analogy relates to something in our everyday lives.

If you can imagine adding items to, or removing items from, a Stack of…literally anything…you’ll realize that every (sane) person naturally obeys the LIFO rule.

We add things to the top of a stack. We remove things from the top of a stack. We never add things to, or remove things from, the bottom of the stack. That’s just crazy.

Note: We can use JavaScript Arrays to implement a basic stack. Array#push adds to the top of the stack and Array#pop will remove from the top of the stack. In the exercise that follows, we’ll build our own Stack class from scratch (without using any arrays). In an interview setting, your evaluator may be okay with you using an array as a stack.

What is a Queue?

Queues are a First In First Out (FIFO) data structure. The first Node added to the queue is always the first Node to be removed.

The name Queue comes from this characteristic, as it is helpful to visualize this data structure as a horizontal line of items with a beginning and an end. Personally, I like to think of a Queue as the line one waits on for an amusement park, at a grocery store checkout, or to see the teller at a bank.

If you can imagine a queue of humans waiting…again, for literally anything…you’ll realize that most people (the civil ones) naturally obey the FIFO rule.

People add themselves to the back of a queue, wait their turn in line, and make their way toward the front. People exit from the front of a queue, but only when they have made their way to being first in line.

We never add ourselves to the front of a queue (unless there is no one else in line), otherwise we would be “cutting” the line, and other humans don’t seem to appreciate that.

Note: We can use JavaScript Arrays to implement a basic queue. Array#push adds to the back (enqueue) and Array#shift will remove from the front (dequeue). In the exercise that follows, we’ll build our own Queue class from scratch (without using any arrays). In an interview setting, your evaluator may be okay with you using an array as a queue.

Stack and Queue Properties

Stacks and Queues are so similar in composition that we can discuss their properties together. They track the following three properties:

Stack Properties | Queue Properties:

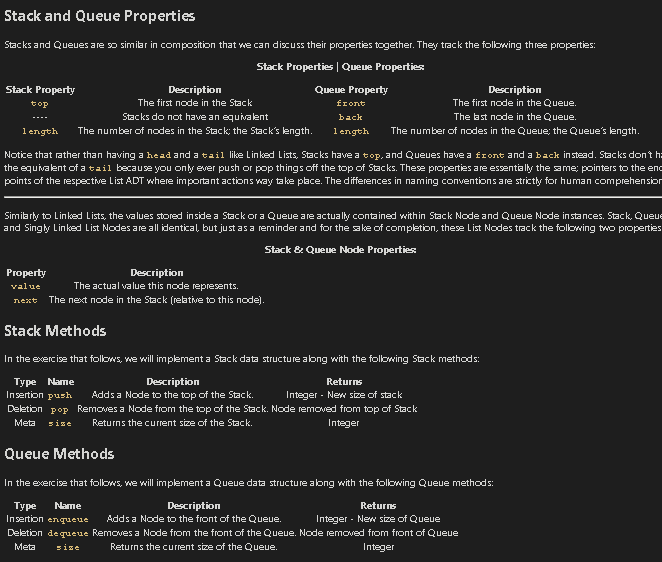
Notice that rather than having a head and a tail like Linked Lists, Stacks have a top, and Queues have a front and a back instead. Stacks don’t have the equivalent of a tail because you only ever push or pop things off the top of Stacks. These properties are essentially the same; pointers to the end points of the respective List ADT where important actions way take place. The differences in naming conventions are strictly for human comprehension.

Similarly to Linked Lists, the values stored inside a Stack or a Queue are actually contained within Stack Node and Queue Node instances. Stack, Queue, and Singly Linked List Nodes are all identical, but just as a reminder and for the sake of completion, these List Nodes track the following two properties:

Time and Space Complexity Analysis

Before we begin our analysis, here is a quick summary of the Time and Space constraints of each Stack Operation.

Data Structure Operation Time Complexity (Avg)Time Complexity (Worst)Space Complexity (Worst)AccessΘ(n)O(n)O(n)SearchΘ(n)O(n)O(n)InsertionΘ(1)O(1)O(n)DeletionΘ(1)O(1)O(n)

Before moving forward, see if you can reason to yourself why each operation has the time and space complexity listed above!

Time Complexity — Access and Search

When the Stack ADT was first conceived, its inventor definitely did not prioritize searching and accessing individual Nodes or values in the list. The same idea applies for the Queue ADT. There are certainly better data structures for speedy search and lookup, and if these operations are a priority for your use case, it would be best to choose something else!

Search and Access are both linear time operations for Stacks and Queues, and that shouldn’t be too unclear. Both ADTs are nearly identical to Linked Lists in this way. The only way to find a Node somewhere in the middle of a Stack or a Queue, is to start at the top (or the back) and traverse downward (or forward) toward the bottom (or front) one node at a time via each Node’s next property.

This is a linear time operation, O(n).

Time Complexity — Insertion and Deletion

For Stacks and Queues, insertion and deletion is what it’s all about. If there is one feature a Stack absolutely must have, it’s constant time insertion and removal to and from the top of the Stack (FIFO). The same applies for Queues, but with insertion occurring at the back and removal occurring at the front (LIFO).

Think about it. When you add a plate to the top of a stack of plates, do you have to iterate through all of the other plates first to do so? Of course not. You simply add your plate to the top of the stack, and that’s that. The concept is the same for removal.

Therefore, Stacks and Queues have constant time Insertion and Deletion via their push and pop or enqueue and dequeue methods, O(1).

Space Complexity

The space complexity of Stacks and Queues is very simple. Whether we are instantiating a new instance of a Stack or Queue to store a set of data, or we are using a Stack or Queue as part of a strategy to solve some problem, Stacks and Queues always store one Node for each value they receive as input.

For this reason, we always consider Stacks and Queues to have a linear space complexity, O(n).

When should we use Stacks and Queues?

At this point, we’ve done a lot of work understanding the ins and outs of Stacks and Queues, but we still haven’t really discussed what we can use them for. The answer is actually…a lot!

For one, Stacks and Queues can be used as intermediate data structures while implementing some of the more complicated data structures and methods we’ll see in some of our upcoming sections.

For example, the implementation of the breadth-first Tree traversal algorithm takes advantage of a Queue instance, and the depth-first Graph traversal algorithm exploits the benefits of a Stack instance.

Additionally, Stacks and Queues serve as the essential underlying data structures to a wide variety of applications you use all the time. Just to name a few:

Stacks

The Call Stack is a Stack data structure, and is used to manage the order of function invocations in your code.
Browser History is often implemented using a Stack, with one great example being the browser history object in the very popular React Router module.
Undo/Redo functionality in just about any application. For example:
When you’re coding in your text editor, each of the actions you take on your keyboard are recorded by pushing that event to a Stack.
When you hit [cmd + z] to undo your most recent action, that event is poped off the Stack, because the last event that occured should be the first one to be undone (LIFO).
When you hit [cmd + y] to redo your most recent action, that event is pushed back onto the Stack.

Queues

Printers use a Queue to manage incoming jobs to ensure that documents are printed in the order they are received.
Chat rooms, online video games, and customer service phone lines use a Queue to ensure that patrons are served in the order they arrive.
In the case of a Chat Room, to be admitted to a size-limited room.
In the case of an Online Multi-Player Game, players wait in a lobby until there is enough space and it is their turn to be admitted to a game.
In the case of a Customer Service Phone Line…you get the point.
As a more advanced use case, Queues are often used as components or services in the system design of a service-oriented architecture. A very popular and easy to use example of this is Amazon’s Simple Queue Service (SQS), which is a part of their Amazon Web Services (AWS) offering.
You would add this service to your system between two other services, one that is sending information for processing, and one that is receiving information to be processed, when the volume of incoming requests is high and the integrity of the order with which those requests are processed must be maintained.

If you found this guide helpful feel free to checkout my other articles:

A list of all of my articles to link to future posts
You should probably skip this one… seriously it’s just for internal use!bryanguner.medium.com

Further resources:

bgoonz’s gists
Instantly share code, notes, and snippets. Web Developer, Electrical Engineer JavaScript | CSS | Bootstrap | Python |…gist.github.com

Web-Dev-Resource-Hub
Edit descriptionweb-dev-resource-hub.netlify.app

Here’s a live code editor where you can mess with any of the examples:

web-dev-hub

Search This Blog